Math Kangaroo is an international mathematics competition that encourages K-12 students to strengthen their problem-solving skills in a fun and engaging way. For nearly 30 years, Math Kangaroo USA, NPF has proudly organized the competition in the United States, inspiring a love for math and reaching hundreds of thousands of students across the country.
Each year, member countries of Association Kangourou Sans Frontières submit hundreds of problem proposals for the annual competition. However, only 168 problems make the final selection across six levels.
What exactly are the selection committees looking for? First, problems must align with curricular guidelines to ensure they’re appropriate for each grade level. But just as importantly, they can’t be typical “textbook problems.” Instead, they need to spark students’ interest by connecting to real life and offering a bit of a challenge.
Creativity plays a role not only in solving the problem but also in crafting it.
The Math Kangaroo test includes 24 questions for grades 1-4 (right now, kindergarteners compete at the 1st grade level) and 30 questions for grades 5-12, with progressive difficulty and point value. There are three types of questions: 3-point, 4-point, and 5-point.
• 3-point questions are the easiest, focusing on fundamental skills.
• 4-point questions require more problem-solving and offer a moderate challenge.
• 5-point questions are the toughest, designed to test critical thinking and creativity.
This structure helps motivate students to progress and rewards different levels of mathematical ability.
I would like to present three problems from the 2025 competition for our younger levels. All three of these problems relate to basic algebraic concepts, but we are not expecting students in these grades to be writing equations. Instead, I suggest that these problems can be solved by drawing appropriate pictures.
The first problem is for grades 1 and 2. It is worth 4 points.
There were 12 pieces of fruit on the table. Vera removed 2 pears, 4 apples, and half of the oranges. Now there are only oranges left on the table. How many oranges are left?
(A) 1 (B) 2 (C) 3 (D) 4 (E) 6
To solve this problem, the student might draw a picture of 12 pieces of fruit.

The next step would be to mark the 2 pears and 4 apples, and realize that everything else (everything else that was taken and what is left) is oranges. This can be done by marking with letters, P for “pear,” A for “apple,” and O for “orange,” or by making the drawing more detailed. If the problem is being solved outside the competition, such as for practice at home or in the classroom, color can help.
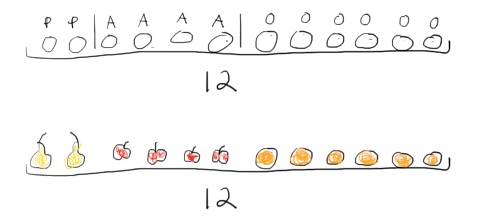
From this, one can tell that if half of the oranges were taken, half are left, so 3 oranges are left.
Here is a problem for grades 3 and 4. It is also a 4-point question.
In the petting zoo, Rene feeds 6 sheep. She gives them a total of 210 grams of dry food for lunch. She gives the smallest sheep twice as much food as she gives to each of the others. How much does the smallest sheep get?
(A) 55 grams (B) 60 grams (C) 70 grams (D) 75 grams (E) 80 grams
Some questions, such as this one, provide a picture that can help the student work the problem.
It can be labeled with how many “portions” each sheep gets, showing that there is a total of 7 portions.

Then it is easy to see that 210 needs to be divided by 7. As the final step, the student hopefully remembers to multiply by 2 to get the final answer of 60 grams.
And this is a problem for grades 5 and 6. It is a 5-point question.
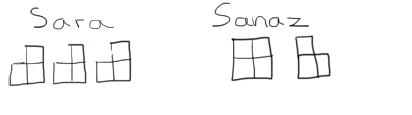
Sara had three times as many chocolate bars as Sanaz. Sara then gave a quarter of her bars to Sanaz. Sara now has six more bars than Sanaz. How many more bars than Sanaz did Sara have originally?
(A) 36 (B) 30 (C) 27 (D) 24 (E) 20
As a 5-point problem, it’s very challenging. Again, we are not expecting students of this age to be writing algebraic equations, so we are going to solve it by drawing.
Sara had three times as many bars as Sanaz, so we can start with three boxes for Sara and one for Sanaz.

She gave a quarter of them to Sanaz, so we can divide each box into fourths and mark one-fourth in each as the portion she gave.

After she gives the bars to Sanaz, the distribution will look like this:
We now see that at the end, Sara has 9 small parts and Sanaz has 7. The difference between the two parts corresponds to six chocolate bars, so each part is equal to 3 bars.
Looking at our second picture, we see that Sara originally had 12 × 3 = 36 bars and Sanaz 4 ⨉ 3 = 12. The difference at the beginning was 36 – 12 = 24 bars.
Math Kangaroo competition
The Math Kangaroo competition is full of intriguing problems, ones that students can solve with creativity and thoughtful reasoning, using the skills they already know. Our goal is to inspire learning, not just competition.
While the problems can be challenging, they’re designed to be a fun challenge. They are an opportunity to think in new ways and enjoy the process. Many students have shared how much they love tackling these problems, and we hope to continue sparking that enthusiasm.




Leave a Reply