Hints:

1.Try solving a simpler version first!
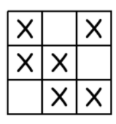
A 3×3 grid solution might look like this:

X X _

X _ X

_ X X

Now think about how this pattern could extend to a 4×4 grid.

2. Start by filling the left column and the bottom row,
but leave the bottom-left corner empty.

What would be a clever way to complete the rest of the grid?
Look for a pattern that makes every row and column meet the puzzle’s rules!

Solution:

Solving this puzzle for any size grid is actually part of a much deeper, unsolved problem in mathematics! But don’t let that stop you—exploring this puzzle is a great way to learn and discover new patterns.

Let’s say the grid has m rows and n columns.

What We Know So Far:

• 1 or 2 rows: The best you can do is place m + n − 1 X’s.

• 3 rows: You can place m + n X’s. The 3×3 grid is a great starting point, and for more columns, you can just add one X in each new column.

The 3-row strategy looks different from the 1–2 row cases. So what happens when we try 4 or more rows?

A New Strategy:

Try this for an m × m grid:

• Fill the leftmost column, skipping just the bottom square.

• Then, for each of the other columns, place two X’s: one in the bottom row and one somewhere else.

This gives you a total of
(m − 1) + 2 × (m − 1) = 3 × (m − 1) X’s.

If the grid has more columns than rows (m < n), we can extend the pattern by adding one X per extra column. This gives a general formula:
n + 2m − 3 X’s.

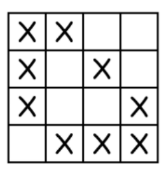
This formula matches every successful example we’ve found so far—for any size grid with more than 1 row!