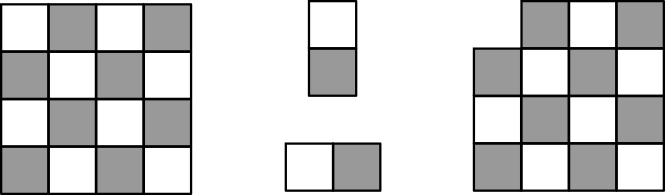Hints:

1. Both challenge boards contain an even number of squares.

2. A domino always covers one white square and one black square.

3. So, for a full tiling to be possible, the number of white and black squares on the board must be exactly equal.

4. Carefully count the number of black and white squares remaining after removing any pieces—do they still match?

What do you notice about the balance of colors on each board?

Solution:

There are two important ideas (or formulas) to consider for solving this puzzle.

1. Total Number of Squares (Even vs. Odd):
Since each domino covers exactly two squares, every time a domino is placed, it reduces the number of uncovered squares by two—an even number.

• So, if you start with an even number of squares, it’s possible to end with zero uncovered squares (i.e., completely cover the board).

• If you start with an odd number of squares, it’s impossible to end with zero, since you’ll always have one left over.

Looking at the two introductory examples:

• The first board has an even number of squares, so it’s numerically possible to tile it completely.

• The second board has an odd number of squares, so it’s impossible to cover it fully with dominoes.

2. Color Balance (An Invariant):
Each domino always covers one dark square and one light square. So, the difference between the number of dark and light squares stays constant as you place dominoes. This constant difference is called an invariant.

• On the first challenge board, there are 8 dark squares and 6 light squares. The difference is 2. This difference never changes, so the board can never be fully covered by dominoes (which would require the difference to become 0).

• On the second board, there are 7 dark and 7 light squares—difference 0. That gives it a chance to be completely covered, and in fact, it’s easy to find a tiling that works.

Exploration:

This color difference, called an invariant, is a powerful tool. Only when the difference is zero is it potentially possible to tile the board completely.
Even then, tiling might still fail if, for example, a square becomes isolated (like a corner square surrounded by missing squares). But generally, if the color difference is 0 and the total number of squares is even, there’s a good chance the board can be covered with dominoes.