Solution:

To solve this puzzle, we translate it into a graph problem where:

• Land areas become nodes (vertices), and

• Bridges become edges (connections) between those nodes.

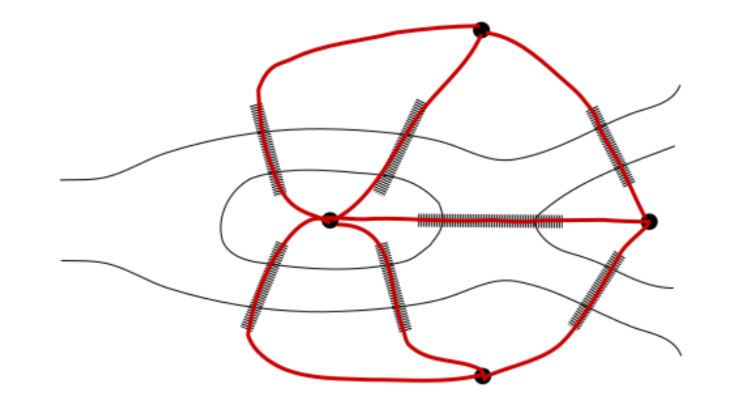
This type of problem relates to finding a trail that uses every edge exactly once, known in mathematics as an Eulerian path.

Key Rule:

A graph can have a trail that uses every edge exactly once only if it has:

• 0 or 2 nodes with an odd number of edges (bridges).

If more than two nodes have an odd number of bridges connected to them, such a trail is impossible.

Applying this to the Puzzle:

In this case:

• All four nodes (land areas) have an odd number of bridges.

• That means there are 4 nodes with odd degrees, which violates the rule.

Conclusion:

Because there are more than two nodes with an odd number of edges, it is impossible to create a parade route that crosses each bridge exactly once without repetition.

Exploration:

What Happens If You Add One More Bridge?

What if we added just one more bridge anywhere across the river?

That single change would turn one of the land areas (nodes) from having an odd number of bridges to an even number.

Why This Helps:

• Originally, all four nodes had an odd number of edges (bridges).

• Adding one new bridge connects two nodes, changing their degrees from odd to even.

• After this change, only two nodes will have an odd number of edges.

According to graph theory, having exactly two nodes with odd degree makes it possible to find a trail that uses each bridge exactly once (an Eulerian path).

Conclusion:

By adding just one more bridge, you make it mathematically possible to plan a full parade route that crosses every bridge once and only once. Problem solved!